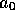 を実数、
を実数、 を実数を成分とする3次元ベクトルとするとき
を実数を成分とする3次元ベクトルとするとき




問2 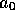 を実数、
を実数、 を実数を成分とする3次元ベクトルとするとき
を実数を成分とする3次元ベクトルとするとき
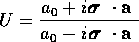
で定義される 行列を考える。
行列を考える。
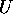 がユニタリーかつユニモジュラーであること
を証明せよ。
がユニタリーかつユニモジュラーであること
を証明せよ。
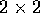 ユニタリー・ユニモジュラー行列
は、
3次元での 回転 を表す。
ユニタリー・ユニモジュラー行列
は、
3次元での 回転 を表す。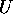 に対応する回転軸と回転角を、
に対応する回転軸と回転角を、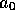 ,
,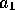 ,
,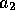 および
および
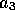 を用いて求めよ。
を用いて求めよ。
[解答]
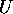 の エルミート共役行列 は
の エルミート共役行列 は
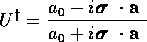
であるから、

となり、行列 はユニタリーである。
はユニタリーである。
また、行列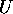 の行列式は
の行列式は
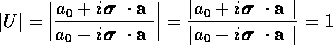
であるから、行列 はユニモジュラーである。
ただし、分母分子それぞれの行列式
はユニモジュラーである。
ただし、分母分子それぞれの行列式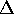 がともに
がともに
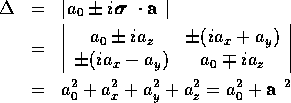
となることを用いた。
 の行列要素を計算しよう。
の行列要素を計算しよう。
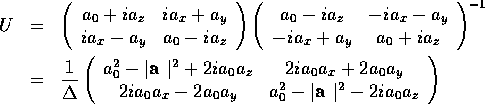
教科書の式(3.3.10)より、
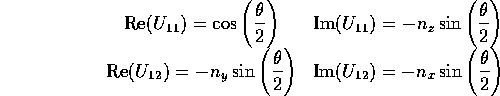
であるから、回転角は
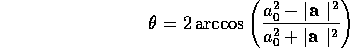
回転軸は
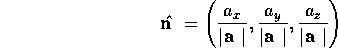
となる。



