問２９ 原点に置かれた スピン
の 原子核
が、外部から不均一な
電場を受けている。基礎になる 電気４重極相互作用
は
のようにとることができる。ここで
はラプラス方程式を
満たす
静電ポテンシャルであり、座標軸は
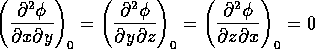
となるように選ばれている。このとき相互作用エネルギーは
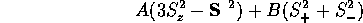
のように書くことができることを示し、
と
を
などで表せ。エネルギー固有ケットを（
,
を用いて）定め、対応するエネルギー固有値を求めよ。縮退はあるか。
核四極子共鳴
［解答］
まず、
をもとめよう。
スピン演算子
は
とはしご演算子であらわせるので
を用いると、
をえる。 よって、
と書ける。
ハミルトニアン
を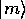
,
を基底ケットに
とって行列表示すると
となる。固有方程式は
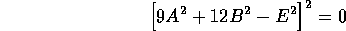
となって、エネルギー固有値は２重に縮退している。
この縮退は、ハミルトニアンの 時間反転不変性
の結果、角運動量
が半整数の系に必ず存在する
クラマースの縮退
の例となっている。
（教科書４．４節参照）
時間反転をすれば、 スピン
の向きは逆になるがハミルトニアンは不変である。
したがって、スピン逆向きの状態は元の状態と同じエネルギーを持つ固有状態となる。
また、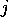
が半整数のときは、
のように
が
ゼロに成る状態を作れないので、スピン逆向きの状態は元の状態とは
異なる状態となる。よって、クラマースの縮退が起こる。
このことを本問の固有ケットについて確かめよ。