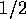 の フェルミオン
が、無限に高い障壁ポテンシャル
(
の フェルミオン
が、無限に高い障壁ポテンシャル
(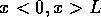 に対して
に対して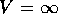 、
、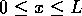 に対
して
に対
して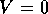 )
の間を1次元的に運動している。
)
の間を1次元的に運動している。




問7 2個の同一種類のスピン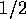 の フェルミオン
が、無限に高い障壁ポテンシャル
(
の フェルミオン
が、無限に高い障壁ポテンシャル
(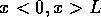 に対して
に対して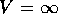 、
、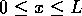 に対
して
に対
して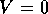 )
の間を1次元的に運動している。
)
の間を1次元的に運動している。
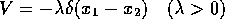
で近似できる引力ポテンシャルを通じて2粒子が相互作用していると仮定する。 このような特異的ポテンシャルに対しても摂動論が有効であると仮定して、 (a),(b)で得られたエネルギー準位がどのようになるかを半定量的に議論せよ。
[解答] まず、一粒子状態のエネルギー固有関数とエネルギー固有値を 求めると
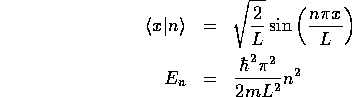
となる。また、問題の粒子はスピン なので、
全体の波動関数は粒子の入れ替えに対して 反対称
である。
なので、
全体の波動関数は粒子の入れ替えに対して 反対称
である。
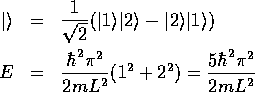
となる。
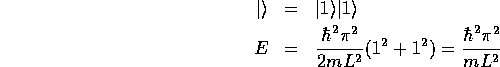
となる。
 は、
は、
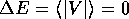
となる。基底状態の波動関数が反対称的なので2つの粒子は同じ位置に 存在することはない。したがって、デルタ関数型の摂動によっては エネルギーが変化しない。このことは、摂動論が成り立つ限り 高次の摂動に対しても正しい。
(b.)の基底状態に対して、
1次の摂動論でエネルギーのずれ は、
は、
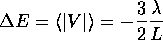
となる。 基底状態の波動関数が対称的なので2つの粒子は同じ位置に 存在できる。したがって、デルタ関数型の引力ポテンシャルによって エネルギーが下がる。



