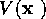 によって、ある固定された中心に
束縛
されている。 時間反転不変性
を用い、任意のエネルギー固有状態に対して
によって、ある固定された中心に
束縛
されている。 時間反転不変性
を用い、任意のエネルギー固有状態に対して




問10 スピンを持たない粒子が、 対称性
がなくエネルギー準位に 縮退
を作らないポテンシャル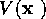 によって、ある固定された中心に
束縛
されている。 時間反転不変性
を用い、任意のエネルギー固有状態に対して
によって、ある固定された中心に
束縛
されている。 時間反転不変性
を用い、任意のエネルギー固有状態に対して
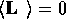
を証明せよ。(これは、 軌道角運動量の消失 と呼ばれている。) このような非縮退固有状態の波動関数が
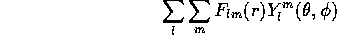
のように展開されたとすると、 に対してどのような
位相の制限 が
つくか。
に対してどのような
位相の制限 が
つくか。
[解答]
a.
時間反転不変な系では、固有状態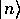 は
は
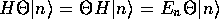
となるので、 と
と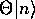 は同じエネルギーを持つ。
よって、エネルギー準位に縮退がなければ、位相因子を除いて
は同じエネルギーを持つ。
よって、エネルギー準位に縮退がなければ、位相因子を除いて
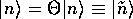
とおける。 軌道角運動量 演算子 は、時間反転に関して奇
は、時間反転に関して奇
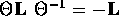 であるから、
恒等式(4.4.36)より
であるから、
恒等式(4.4.36)より
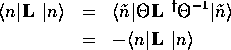
となり、

と結論される。 結晶中の電子のように、ポテンシャルの対称性が低いときは、軌道角運動量の消 失により、軌道磁気モーメントがゼロになることがある。
非縮退固有状態の波動関数を
とすると、時間反転した波動関数は
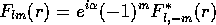
が成り立つ必要がある。



