



Next:
Up: 5 近似法
Previous: 5 近似法
VISIT MY BOOKSHELF
http://www.iitaka.org/
問1 調和振動子
(1次元)が摂動 を受ける。
を受ける。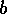 は実定数である。
は実定数である。
- a.
- 基底状態のエネルギーのずれを有限な答えを与える最低次
まで計算せよ。
- b.
- この問題を厳密に解き(a.)で得た結果と比較せよ。
[証明せずに
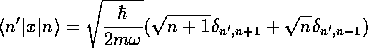
を仮定してよい。]
[解答]
- a.
-
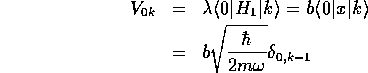
であることに注意すれば、
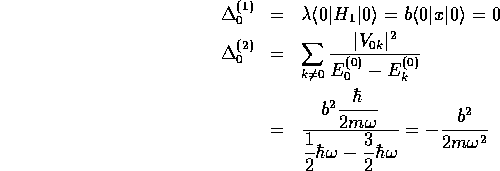
となる。
- b.
- 全ハミルトニアンを書き直すと、
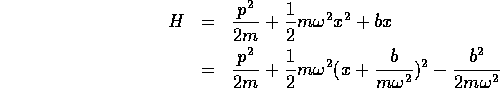
となって、原点のx-座標を( )、エネルギー
を(
)、エネルギー
を(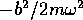 )だけ
ずらした調和振動子のハミルトニアンになる。よって、すべてのエネルギー
固有状態のエネルギーは(
)だけ
ずらした調和振動子のハミルトニアンになる。よって、すべてのエネルギー
固有状態のエネルギーは(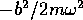 )だけ下がる。
)だけ下がる。




Next:
Up: 5 近似法
Previous: 5 近似法
Iitaka Toshiaki
1996年07月27日 11時31分42秒
 を受ける。
を受ける。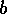 は実定数である。
は実定数である。




 を受ける。
を受ける。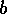 は実定数である。
は実定数である。
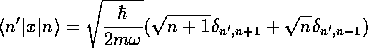
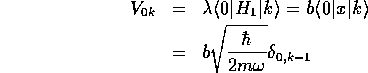
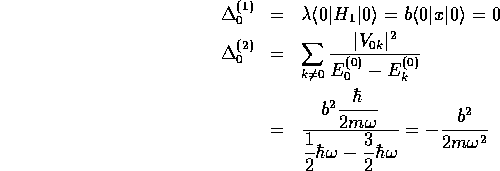
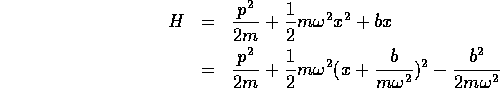
 )、エネルギー
を(
)、エネルギー
を(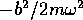 )だけ
ずらした調和振動子のハミルトニアンになる。よって、すべてのエネルギー
固有状態のエネルギーは(
)だけ
ずらした調和振動子のハミルトニアンになる。よって、すべてのエネルギー
固有状態のエネルギーは(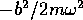 )だけ下がる。
)だけ下がる。



