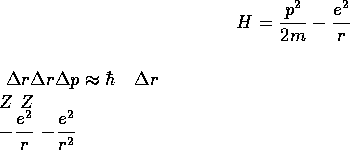 である1次元 調和振動子
を考える。
この系は
である1次元 調和振動子
を考える。
この系は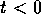 で基底状態にあることが分かっている。
で基底状態にあることが分かっている。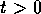 では 時間依存性のあるポテンシャル
では 時間依存性のあるポテンシャル




問22 古典的角振動数が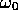 である1次元 調和振動子
を考える。
この系は
である1次元 調和振動子
を考える。
この系は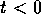 で基底状態にあることが分かっている。
で基底状態にあることが分かっている。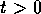 では 時間依存性のあるポテンシャル
では 時間依存性のあるポテンシャル
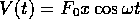
が加わる。ここで は空間的にも時間的にも一定値であ
る。時間を含む摂動論を
用い有限な解を与える最低次で期待値
は空間的にも時間的にも一定値であ
る。時間を含む摂動論を
用い有限な解を与える最低次で期待値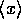 の表式を時間の関数とし
て
求めよ。この手続きは
の表式を時間の関数とし
て
求めよ。この手続きは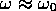 のときも有効か。
のときも有効か。
[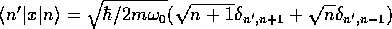 を用いるとよい。]
を用いるとよい。]
[解答] 時間に依存した1次の摂動論を用いる。
添え字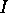 で相互作用表示であることを示せば、
で相互作用表示であることを示せば、
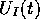 の展開式(5.6.17)より
の展開式(5.6.17)より
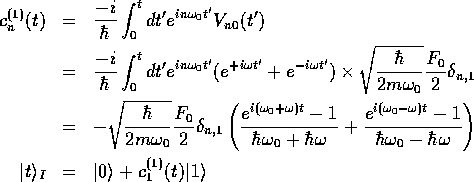
となる。 したがって、位置の期待値は
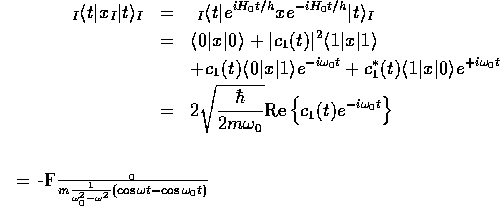
となる。
この手続きは のときには有効でない。
問25の解答からも分かるように、この問題のn次の展開係数
のときには有効でない。
問25の解答からも分かるように、この問題のn次の展開係数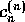 は
分母に
は
分母に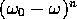 を含むので
を含むので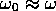 の領域では
高次の摂動項が重要になってくる。したがって、高次の摂動項を足し合わせる
必要がある。
このことは、古典的調和振動子が固有振動数に近い振動数の外力を受けると 共鳴
を起こして振幅がどんどん大きくなってゆくことに対応する。
の領域では
高次の摂動項が重要になってくる。したがって、高次の摂動項を足し合わせる
必要がある。
このことは、古典的調和振動子が固有振動数に近い振動数の外力を受けると 共鳴
を起こして振幅がどんどん大きくなってゆくことに対応する。