 の 2準位系
を考える。2準位系を結ぶ時間に依存する
次のようなポテンシャルがある:
の 2準位系
を考える。2準位系を結ぶ時間に依存する
次のようなポテンシャルがある:




問30  の 2準位系
を考える。2準位系を結ぶ時間に依存する
次のようなポテンシャルがある:
の 2準位系
を考える。2準位系を結ぶ時間に依存する
次のようなポテンシャルがある:
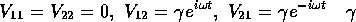
 では下の準位のみに状態が分布していたこと---すな
わち
では下の準位のみに状態が分布していたこと---すな
わち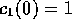 ,
,
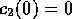 ---が分かっている。
---が分かっている。
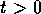 での
での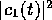 ,
,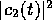 を、連立微分方程式
を、連立微分方程式

を厳密に解いて求めよ。[ ]
]
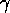 が小さい値のとき比較せよ。
次の二つの場合を別々に扱え:(i)
が小さい値のとき比較せよ。
次の二つの場合を別々に扱え:(i)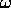 が
が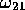 と非常に異なる場合、
(ii)
と非常に異なる場合、
(ii)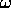 が
が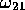 と近い場合
と近い場合
[解答]
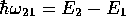 とすれば、
とすれば、
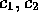 に関する連立微分方程式は
に関する連立微分方程式は
となる。
この方程式を互いに代入して、 のみ、
のみ、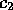 のみの微分方程式を
作ると
のみの微分方程式を
作ると
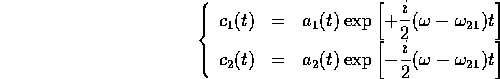
を行い、この変換を式(24)に代入して
 と
と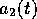 に対する微分方程式
に対する微分方程式
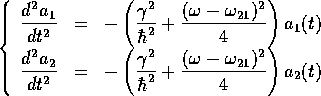
を得る。
 と
と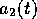 の一般解は
の一般解は
と書ける。ただし

である。
となる。
さて、初期条件と式(26)から
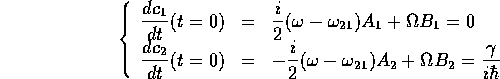
を得る。 よって、4つの積分定数は
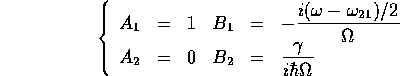
となる。したがって、遷移振幅は
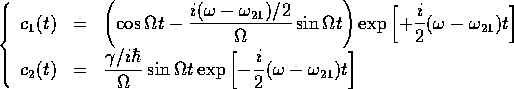
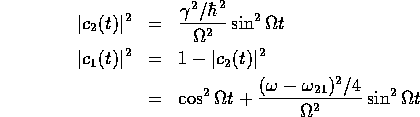
が導かれる。
 と
と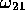 が非常に異なる場合、
時間に依存した摂動論により
が非常に異なる場合、
時間に依存した摂動論により
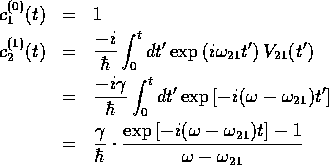
となる。
 の場合、
時間に依存した摂動論により
の場合、
時間に依存した摂動論により
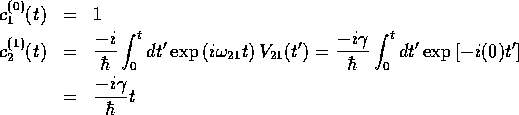
となる。



