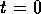問１１
１次元 調和振動子
のポテンシャル中にある１粒子を考察する。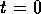
で、
状態ベクトルが
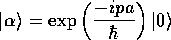
のように与えられたとする。ここで
は運動量演算子であ
り、
は長さの
次元を持つ量である。 ハイゼンベルク表示 を用いて、 期待値
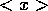を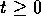
に対し計算せよ。
［解答］ 問１０の a.の結果より、ハイゼンベルク表示の位置演算子は
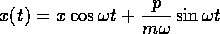
と書けることと、運動量演算子
が無限小の
平行移動演算子
であること
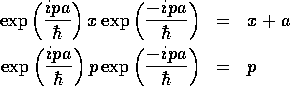
を用いて、
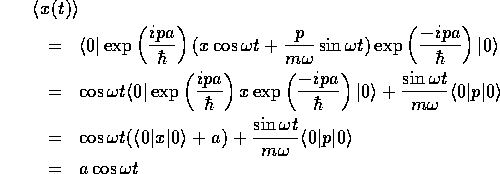
を得る。
時刻
での波動関数は
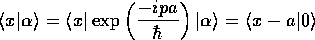
となるので（問１２参照）、
は古典力学でバネをつりあいの位置から
だけ
ずらした状態に対応する。したがって、振動子の位置の期待値は振幅
、
振動数
で振動する。