 の固有状態として定義される:
の固有状態として定義される:




問18 1次元 調和振動子 の コヒーレント状態
は、(非エルミート的な) 消滅演算子  の固有状態として定義される:
の固有状態として定義される:
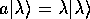
ここで は一般に複素数である。
は一般に複素数である。
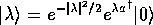
 を
を
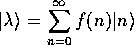
の形に書け。 の
の に関する分布が、ポアソン型であることを示せ。
に関する分布が、ポアソン型であることを示せ。 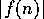 を最大にする
を最大にする の値、したがって
の値、したがって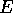 の値
を見出せ。
の値
を見出せ。
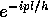 を 基底状態
に作用させることによっても 得られることを示せ。ここで
を 基底状態
に作用させることによっても 得られることを示せ。ここで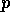 は
運動量演算子で、
は
運動量演算子で、 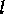 は変位の距離である。
は変位の距離である。
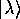 が規格化されていることが、
が規格化されていることが、
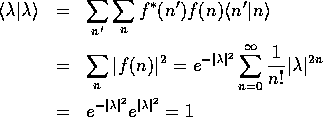
と示される。また、コヒーレント状態であることが、 ベーカー・ハウスドルフの補助定理 を用いて
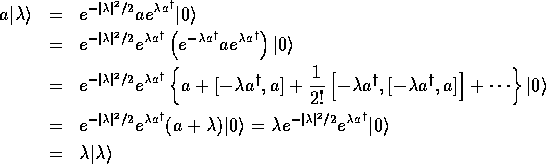
と示される。
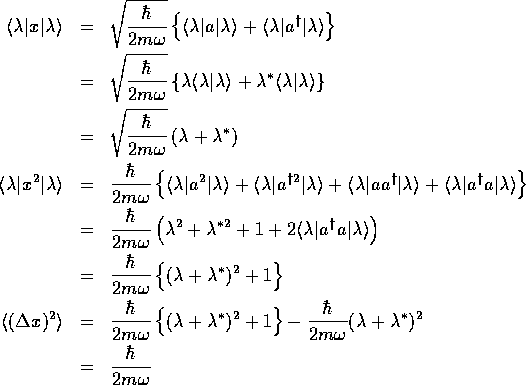
であり、運動量のゆらぎは
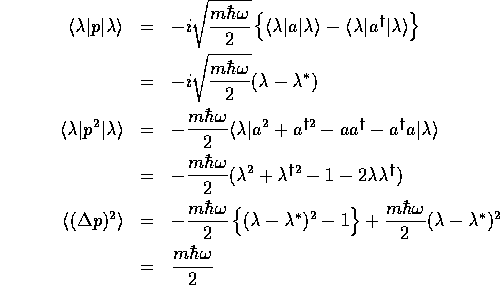
となるので、コヒーレント状態 は、最小不確定
関係
は、最小不確定
関係
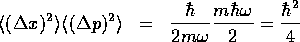
を満たす。 波束の図
 をエネルギー固有状態
をエネルギー固有状態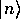 で
展開すると
で
展開すると
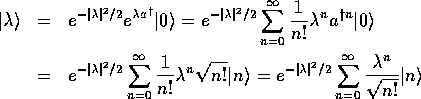
となるので、

を得る。したがって、 の
の  に関するポアッソン型分布
に関するポアッソン型分布
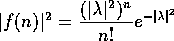
を得る。 ここで両辺の対数をとると
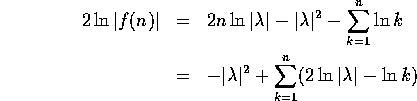
となる。したがって、不等式

すなわち

を満たす限り、 は増加関数
は増加関数
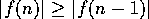
となるので、 が
が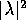 を越えない最大の整数のとき
を越えない最大の整数のとき
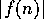 が最大値をとる。したがって、
が最大値をとる。したがって、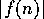 を最大にする
を最大にする の値
および
の値
および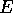 の値は、 ガウスの記号
の値は、 ガウスの記号  を使って
を使って
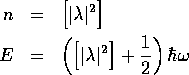
と表される。
 に有限変位の平行移動演
算子
に有限変位の平行移動演
算子
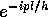 を作用させた状態
を作用させた状態
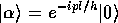
に消滅演算子 を作用させると
を作用させると
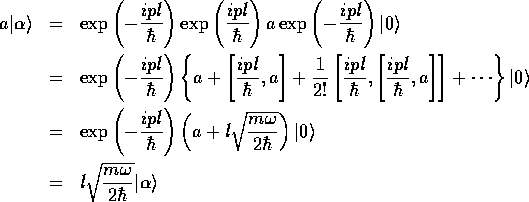
となる。したがって、状態 は、固有値
は、固有値
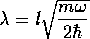
を持つコヒーレント状態である。ただし、上の計算で ベーカー・ハウスドルフの補助定理 と交換関係
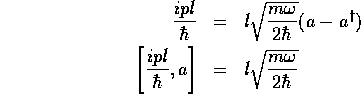
および調和振動子の基底状態の性質 を使った。
を使った。
以上のことから、問11でも扱った、振動する古典的調和振動子に対応する状態
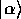 はコヒーレント状態であることが分かる。
はコヒーレント状態であることが分かる。



