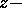 方向を向いた一様な磁場
方向を向いた一様な磁場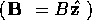 の中を
運動している。
の中を
運動している。




問36
1個の電子が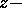 方向を向いた一様な磁場
方向を向いた一様な磁場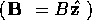 の中を
運動している。
の中を
運動している。
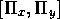 を計算せよ。ただし
を計算せよ。ただし
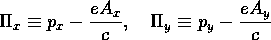
とする。
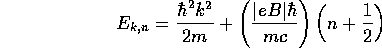
のように表されることを示せ。ここで は
は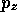 演算子の
連続固有値で、
演算子の
連続固有値で、 はゼロを含む負でない整数である。
はゼロを含む負でない整数である。
[解答]
となる。

にとって、電子のスピンを無視すれば、ハミルトニアンは
のように、 座標のみを含む部分
座標のみを含む部分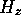 と
と 座標と
座標と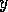 座標を含む部分
座標を含む部分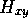 に
分離できる。したがって、全ハミルトニアン
に
分離できる。したがって、全ハミルトニアン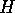 の固有ケット
の固有ケット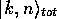 は
は
のような直積の形に書ける。 したがって、部分ハミルトニアンに対する固有方程式
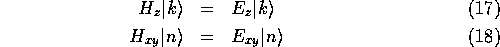
の解が求められれば、全ハミルトニアンに対する固有ケットは
式(16)で与えられ、固有エネルギーは となる。
となる。
部分ハミルトニアン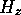 は、1次元の自由粒子のハ
ミルトニアンと
同じ形をしているので、エネルギー固有ケットは 正準運動量演算子
は、1次元の自由粒子のハ
ミルトニアンと
同じ形をしているので、エネルギー固有ケットは 正準運動量演算子 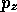 の
固有ケット
の
固有ケット
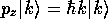
であり、エネルギー固有値は

であることがただちに分かる。
つぎに、部分ハミルトニアン は、
式(15)と設問 a.の結果(12)より、
は、
式(15)と設問 a.の結果(12)より、
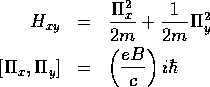
という形をしており、1次元調和振動子のハミルトニアン

と比較して
という対応関係が存在する。
そこで、部分ハミルトニアン は、調和振動子と同じタイプの
エネルギースペクトルを持つ。
じっさい、 「生成消滅演算子」 を
は、調和振動子と同じタイプの
エネルギースペクトルを持つ。
じっさい、 「生成消滅演算子」 を
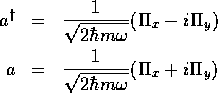
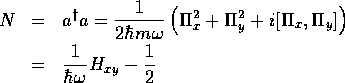
となるので、

と書ける。交換関係(20)を使って、調和振動子と同じ議論を
すれば、ハミルトニアン のエネルギー固有値
のエネルギー固有値
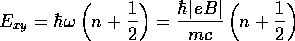
を得る。ただし、 は負でない整数である。
は負でない整数である。
以上まとめると、全ハミルトニアンのエネルギー固有値は
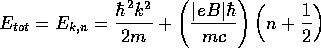
のように表される。ここで は
は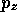 演算子の連続
固有値で、
演算子の連続
固有値で、 はゼロを含む負でない整数である。
はゼロを含む負でない整数である。
調和振動子との対応関係(19)より、磁場中の粒子は
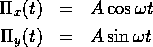
のように 平面方向に円運動していることがわか
る。
平面方向に円運動していることがわか
る。



