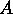 の固有ケット
の固有ケット 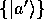 で張られるケット空間を
考える。縮退はないとする。
で張られるケット空間を
考える。縮退はないとする。




問7 エルミート演算子 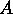 の固有ケット
の固有ケット 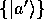 で張られるケット空間を
考える。縮退はないとする。
で張られるケット空間を
考える。縮退はないとする。
[解答]
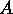 の任意の固有ケット
の任意の固有ケット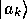 に
問題の演算子
に
問題の演算子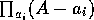 を作用させてみる。
を作用させてみる。
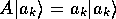
だから、
となる。
問題のケット空間の任意のケット は
は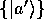 を基底として
を基底として
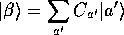
と展開されるので、式(1)をつかって
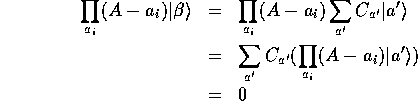
となる。よって、 は
零演算子である。
は
零演算子である。
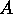 の任意の固有ケット
の任意の固有ケット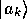 を問題の演算子
を問題の演算子
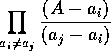 に作用させてみると、
に作用させてみると、
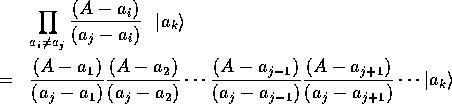
となるので、
 と
と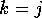 の二つの場合に分けて考える。
の二つの場合に分けて考える。
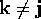
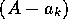 が
ゼロになる。縮退はないので分母はゼロにならない。したがって、
が
ゼロになる。縮退はないので分母はゼロにならない。したがって、
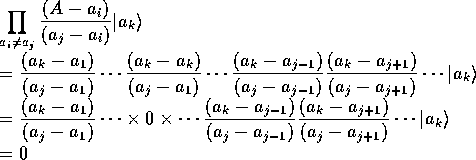
となる。

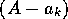 の因子がないので
の因子がないので
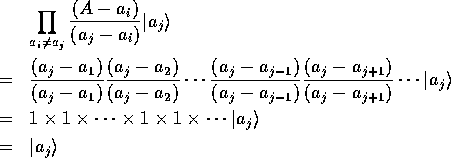
となる。
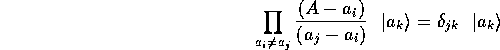
と書ける。
任意のケット に
に
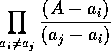 を作用させ
てみよう。
を作用させ
てみよう。
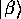 は
は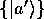 を基底として
を基底として
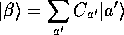
と展開されるので、
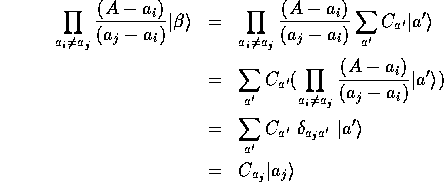
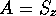 とおくと、
とおくと、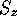 の固有値固有ケットは
の固有値固有ケットは
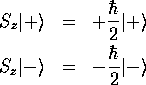
である。
(a.)零演算子は
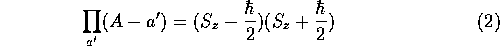
となる。
この演算子を任意のケット に作用させてみよう。
に作用させてみよう。
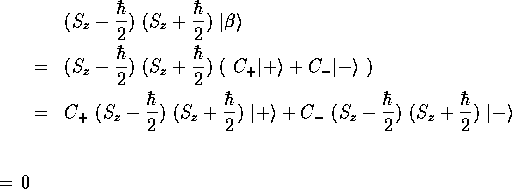
となって、実際に零演算子になっている。
(b.)射影演算子は、 ,
,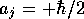 とすれば、
とすれば、
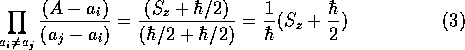
となる。
この演算子を任意のケット に作用させてみよう。
に作用させてみよう。
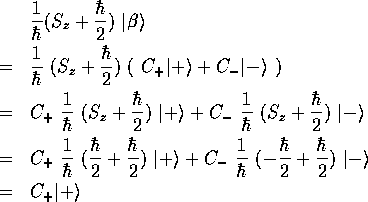
となって、実際に の成分を取り出す
スピン射影演算子
になっている。また、
の成分を取り出す
スピン射影演算子
になっている。また、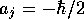 とすれば、
スピン射影演算子は
とすれば、
スピン射影演算子は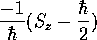 となり、
となり、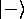 の成分を取り出す演算子になる。
の成分を取り出す演算子になる。



