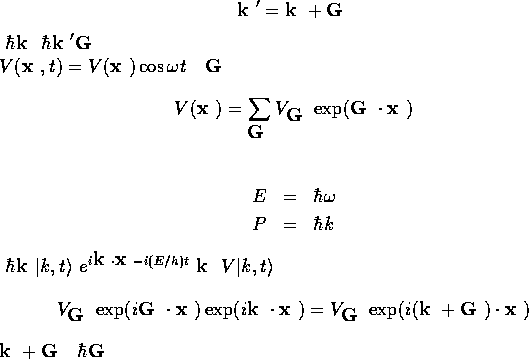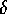 殻ポテンシャル
殻ポテンシャル




による散乱を考える。
 を
を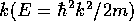 の関数として
決める方程式をたてよ。
の関数として
決める方程式をたてよ。
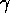 が
が
のように非常に大きいとする。
[解答]
 波に対する
同値な1次元シュレーディンガー方程式
波に対する
同値な1次元シュレーディンガー方程式
を解いて位相のずれを求めよう。
ここで は動径方向の波動関数
は動径方向の波動関数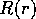 を使って
を使って
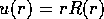 と定義され境界条件
と定義され境界条件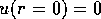 を満たす。
を満たす。
領域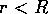 と
と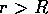 の解は、容易にもとまって
の解は、容易にもとまって
と書ける。ただし、位相のずれを 、殻の内側の
振幅を
、殻の内側の
振幅を
 とおいた。この2つの定数は、
とおいた。この2つの定数は、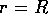 での波動関数の接続条件
での波動関数の接続条件
によって決められる。式(36)は、式(32)を の
周りの微小区間で積分して得られる。
式(33,34)
を
式(35,36)
に代入すると、
の
周りの微小区間で積分して得られる。
式(33,34)
を
式(35,36)
に代入すると、
から、
を得る。
したがって、位相のずれは、 の増加に対して
なめらかに変化する背景散乱による位相のずれ
の増加に対して
なめらかに変化する背景散乱による位相のずれ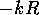 と
共鳴的な振る舞いを表す位相のずれ
と
共鳴的な振る舞いを表す位相のずれ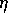 の和
の和
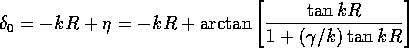
で与えられる。 が共鳴の前後で
が共鳴の前後で だけ変化することに注意せよ。
だけ変化することに注意せよ。
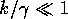 で
で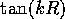 がゼロに近くないので、
がゼロに近くないので、
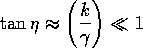
となる。 よって、

となって、s波の位相のずれは剛体球の結果
 と似ている。
問6(a)の結果および教科書の式(7.6.44)を参照せよ。
と似ている。
問6(a)の結果および教科書の式(7.6.44)を参照せよ。
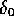 は小さい側から
は小さい側から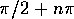 を
横切る。いいかえれば、
を
横切る。いいかえれば、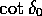 は正の側からゼロを通過する
ことを示そう。式(37)、(38)より
は正の側からゼロを通過する
ことを示そう。式(37)、(38)より
となる。分母は常に負であり、 である
から、
である
から、
のとき
 が正の側からゼロを通過し、共鳴的な振舞い
が起こる。
が正の側からゼロを通過し、共鳴的な振舞い
が起こる。
によって与えられる。これは、球面の内側に閉じ込められた粒子の 状態の
エネルギー
状態の
エネルギー
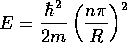
とほぼ一致する。
また、条件(42)が成り立つとき、式(39)より、 粒子が共鳴して殻の内側に一時的に閉じこめられる振幅が非常に大きくなる ことがわかる。
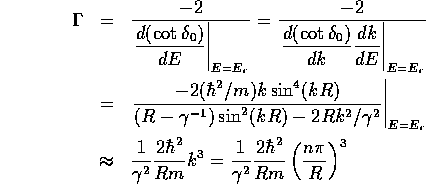
を得る。 が大きくなると、共鳴幅
が大きくなると、共鳴幅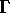 は
は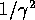 に比例して
小さくなり、共鳴が鋭くなる。
に比例して
小さくなり、共鳴が鋭くなる。